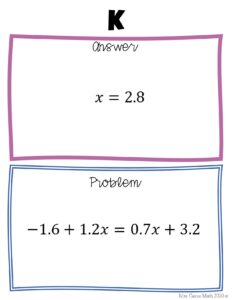
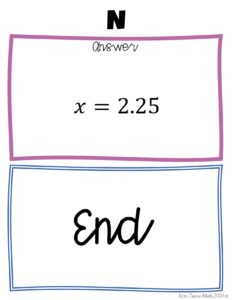
Disclaimer: I did not do my 3-week block this term. However, I did my 8-week, once-a-week, block in which I taught 5 individual lessons. So, I will be demonstrating my assessments in those 5 lessons. 

Azimuth and Altitude Lesson (Lesson 9)

Outcome(s) and Indicator(s)

EU9.4 Analyze human capabilities for exploring and understanding the universe, including technologies and programs that support such exploration.

g. Describe and apply techniques for determining the position of objects in space using horizontal (e.g. azimuth and altitude) and equatorial coordinate systems (e.g., declination and right ascension).

Lesson Description

Students are learning azimuth and altitude for the first time. This lesson is their first introduction. With this lesson, students will understand the context of Azimuth and Altitude and find their measurements either using estimation or a protactor. They will also learn new definitions such as the Azimuth, Altitude, and Zenith. This also taps into their previous knowledge about angles.

Assessment Strategies

Guided Notes: Student Guided Notes

Reasoning: Some students are unable to write full sentences. So, my cooperating teacher searched for a visual guided notes package that fully aligns with what she intends to teach the students about space. This notes package is visually appealing which could engage students to read the notes.

What Kind of Assessment (as, for, of)?

Formative Assessment: Assessment as Learning – Students are responsible for filling up the notes and adding their notes whenever necessary for them. They could add more notes if the teacher has said something important or helpful that was not included in the notes.

Worksheet: Student Worksheet

Reasoning: This is part of the notes package. This worksheet is intended to further practice students’ newly acquired knowledge which is finding the azimuth and altitude in the given domes in the worksheet. If students are struggling to find the measurements just by looking at the visuals, we provide them with two protractors and attach them. This way, it becomes a circle where students can physically measure the azimuth. This method is for adaptation since some students would like to see the measurements in real-time. It could be difficult because some of the measurements are in 3D, meaning they must estimate their measurements. By using two protractors and laying them flat on the table, students can estimate more accurately.

Aside from practicing their azimuth and altitude measurements, students are given four thinking questions to extend their understanding of the topic.

What Kind of Assessment (as, for, of)?

Formative Assessment: Assessment for Learning – student checks their understanding by doing the activity and the four extending questions. This worksheet also informs the teacher of the student’s understanding of measurements and the overall concept of azimuth and altitude (with zenith).

Formative Assessment: Assessment as Learning – Students reflect on their understanding by doing the activity. They could also ask for help from us teachers whenever they need it. So, they are being responsible for their learning as they do the worksheet.

Bloom’s Taxonomy Category

Remembering – They were to remember what azimuth, altitude, and zenith are. They are to remember how to measure azimuth and altitude and the measurement of zenith.

Understanding – They are to understand the measurements and what they represent. They are to understand why the zenith does not need an azimuth measurement.

Applying – They apply their newly acquired knowledge and apply them in different scenarios. For example, Azimuth and Altitude are used heavily in battle royale video games to determine coordinates in the map. This is implied during the lecture.

Complexity

Easy: Guided Notes, First Section of the worksheet

Medium: Extended questions of the worksheet (2nd part)

8.2 Solving Equations Lesson (Math 9)

Outcome(s) and Indicator(s)

P9.2 Model and Solve situational questions using linear equations of the form:

• ax + b = c
• x/a + b = c, a ≠ 0

where a, b, and c are rational numbers.

a. Explain why the equation a/x = b, cannot have a solution of x = 0.

c. Write a linear equation to represent a particular situation.

g. Explain how the preservation of equality is involved in the solving of linear equations.

i. Solve a linear equation symbolically.

j. Analyze the given solution for a linear equation that has resulted in an incorrect solution, and identify and explain the error(s) made.

Lesson Description

Students will be extending their prior knowledge of solving equations from using integers to using rational numbers. Students will tackle different ways of isolating the variable.

Assessment Strategies

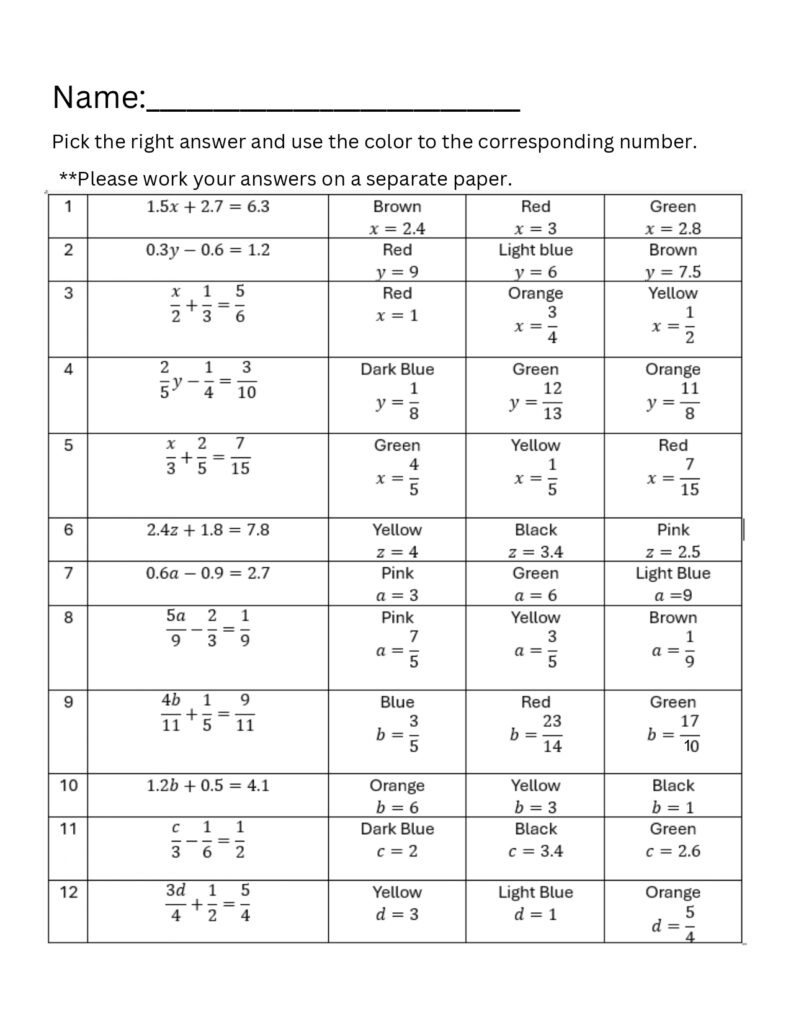
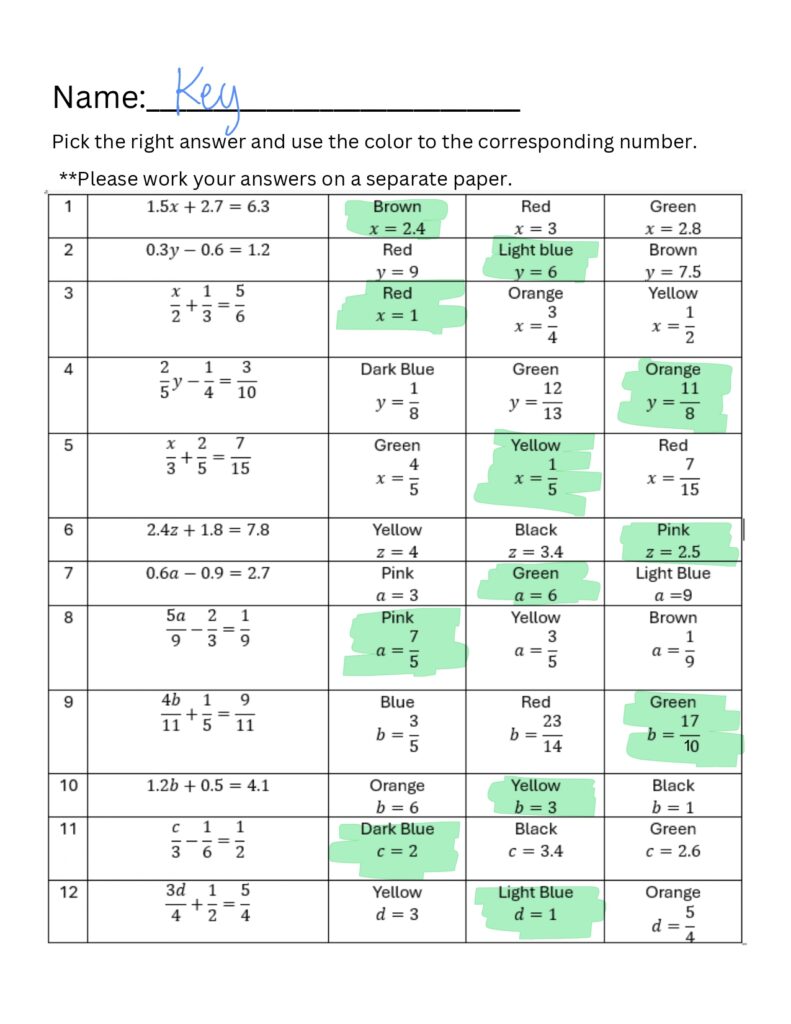
Guided Notes: 8.2 Student Notes

Reasoning: Same with the first lesson. Also, it is easier if the students are following along rather than just looking at how I demonstrate solving the questions. I also make sure to keep asking students what to do next (like they are the ones teaching me how to solve it) so they are fully involved in solving it.

What Kind of Assessment (as, for, of)?

Formative Assessment: Assessment as Learning – Students are responsible for filling up the notes and adding their notes whenever necessary for them. They could add more notes if the teacher has said something important or helpful that was not included in the notes.

Activity: Figure Out the Error: Figure Out the error Activity

Reasoning: One of the indicators states, “Analyze the given solution for a linear equation that has resulted in an incorrect solution, and identify and explain the error(s) made.” This activity assesses their ability to see the error, why is it an error, and how to fix the error.

What Kind of Assessment (as, for, of)?

Formative Assessment: Assessment as Learning – Students assess their ability to solve equations to be able to answer this problem.

Formative Assessment: Assessment for Learning: It also helps me as a teacher to see their level of understanding to inform my teaching practices.

Exit Slips: Exit Slip

Reasoning: Students will be able to think of different ways of solving equations involving fractions. They could even try to show me a demonstration on the exit slip. It is also an adaptation if some students are struggling to put their thinking into words. The second question is simple, yet could become complex because there are no numbers involved, only variables. My cooperating teacher told me that students are struggling whenever the x is in the denominator since they have to do a bunch of operations to fully isolate it. So, I would like to see how students will tackle this question before I proceed with new things. This is not for marks.

What Kind of Assessment (as, for, of)?

Formative Assessment: Assessment for Learning – It informs me on where the student’s understanding is in terms of solving the variable without the use of numbers as well as their order of operations and fractions.

Bloom’s Taxonomy Category

Remembering – remembering their order of operations, the importance of equality, etc.

Understanding – Understanding concepts of isolating the variable and what they understand when they are asked to “solve for x”

Analyzing – The figure out the error activity encourages students to take the given information apart and look for errors and ways to solve and correct the calculation.

Complexity

Easy: Guided notes, exit slips

Medium: Figure out the error activity

8.1 & 8.2 Solving Equations Review Activity (Math 9)

Outcome(s) and Indicator(s)

P9.2 Model and Solve situational questions using linear equations of the form:

• ax + b = c
• x/a + b = c, a ≠ 0
• ax = b
• ax + b = c
• x/a = b, a ≠ 0
• a/x = b, x ≠ 0

where a, b, and c are rational numbers.

c. Write a linear equation to represent a particular situation.

d. Observe and describe a situation relevant to self, family, or community which could be represented by a linear equation.

h. Verify, by substitution, whether or not a given rational number is a solution to a given linear equation.

i. Solve a linear equation symbolically.

Lesson Description

This is a review day for students. However, instead of just reviewing using textbook questions, I have prepared 3+ activities for them to review 8.1 and 8.2 Solving equations. Some adaptations are giving equations with just integers as numbers instead of rational numbers to tone down the difficulty. Additional activities include colouring, solving the maze, and fixing the puzzle to reach different cognitive demands.

Assessment Strategies

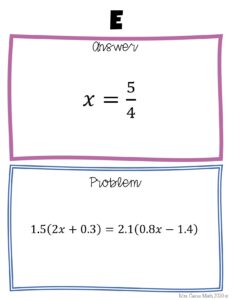
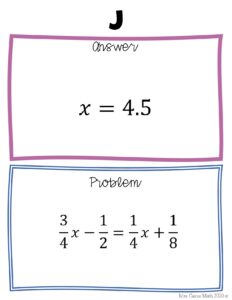
Solving Equation Puzzle: Solving One-Step Equations Puzzle Page 3-16

Reasoning: This puzzle is cut into pieces and I encouraged the students to work on the floor or use a masking tape to put the appropriate pieces together. It is a fun way to do math while doing puzzles. I found that students liked working with the puzzles like a mystery being solved.

Equation Maze: Writing Two-step Equations Maze Page 2

Reasoning: Another fun way to exercise their understanding of creating equations from the given word problems.

Colour by Number Worksheet (Rational Numbers): Solving Two Step Equations Coloring Activity 2 (KEY: Solving Two Step Equations Coloring Activity 2 key)

Reasoning: I am proud of myself because I created this activity. This is a colour-by-number activity. It is like a fun alternative to multiple choice because students would want to produce a great image of the fish taco. This is another fun way of exercising their ability to solve equations while having a relaxed nature of colouring at the same time.

Colour by Number Worksheet (Integers – for adaptation): Two-step equation Coloring activity on pages 3 and 5 (KEY: Two-step equation Coloring activity Page 3 and 5 key)

Reasoning: This is for backup for adaptation. Same colour by number questions but the numbers used are integers instead of rational.

What Kind of Assessment (as, for, of)?

Formative Assessment: Assessment for Learning – it informs me as a teacher where they are before their summative assessment.

Bloom’s Taxonomy Category

Remember – Students remember the things they learned about in previous classes.

Understand – Students understand what they learned to be able to do the activities.

Complexity

Easy: All activities. It is meant to be a fun review day before their exam from my cooperating teacher.

8.4 Equations with Variables on Both Sides (Math 9)

Outcome(s) and Indicator(s)

P9.2 Model and Solve situational questions using linear equations of the form:

• ax = b + cx
• ax + b = cx + d
• a(bx + c) = d(ex + f)

Where a, b, c, d, e, and f are rational numbers.

c. Write a linear equation to represent a particular situation.

h. Verify, by substitution, whether or not a given rational number is a solution to a given linear equation.

i. Solve a linear equation symbolically.

j. Analyze a given solution for a linear equation that has resulted in an incorrect solution, and identify and explain the error(s) made.

Lesson Description

This is the continuation of the Linear Equations unit. Now, students are learning to solve equations when the variables are on both sides. They have learned this before with integers, but now they are learning this unit with rational numbers.

Assessment Strategies

Guided Notes: Student Notes pages 11-12

Reasoning: Same as the previous lessons.

Scavenger Hunt: Scavenger Hunt Cards (Student Worksheet: Solving Equations Scavenger Hunt Student Worksheet)

Reasoning: I am always trying to find ways to make math engaging for students. Scavenger hunt is another idea that I found and applied in my math class. I scattered the cards around the area and had students answer the questions and find the cards with their answers on them. I also made it a competition which even engaged them more. The team with the most cards solved will get a treat next week. I did collect the papers and marked them but they were not for marks. With marking, I made sure to add comments and point out where students stumbled while solving the equation, so they would know for next time. A student also drew an image on their sheets and gave them an extra mark for it!

Worksheet with same questions on Scavenger Hunt activity: Worksheets Not Scavenger Hunt – Copy (KEY: Worksheets Not Scavenger Hunt)

Reasoning: This is for students who do not want to participate in walking around the class and finding cards. it consists of the same questions in the scavenger hunt activity. It is also an adaptation for students with mobility issues. In my case, I do not have students with mobility issues, but if I were to use this activity again in the future, then I would be ready for certain circumstances.

What Kind of Assessment (as, for, of)?

Formative Assessment: Assessment for Learning – Since students are submitting their work, even if they just worked on 1-3 questions, I could infer their level of understanding. This also informs me of where they are at in terms of increasing difficulty in solving equations with rational numbers.

Formative Assessment: Assessment as Learning: Students take notes so they take accountability for their understanding of the topic. They are also allowed to have partners in the scavenger hunt activity, so they look at each other’s calculations and infer whether they got the correct answer.

Bloom’s Taxonomy Category

Remembering – Students are remembering and/or tapping into their previous knowledge to be able to do the activity.

Understanding – Understanding the topic will allow students to do the activity.

Complexity

Easy: They are just using their knowledge from previous classes and applying it in the activity.

9.1 Representing Inequalities

Outcome(s) and Indicator(s)

P9.3 Demonstrate understanding of single variable linear inequalities with rational coefficients including:

• solving inequalities
• verifying
• comparing
• graphing.

a. Observe and describe situations relevant to self, family, or community, including First Nations and Métis communities, that involve inequalities and classify the inequality as being less than, greater than, less than or equal to, or greater than or equal to.

i. Graph the solution of a linear inequality on a number line.

j. Explain why there is more than one solution to a linear inequality.

Lesson Description

Students will re-ignite their prior knowledge about inequality symbols and will apply them with word problem scenarios. They will also tackle abstract thoughts such as the infinite possibilities of an answer for an inequality.

Assessment Strategies

Guided Notes: Student Notes 4-5

Reasoning: Same as the previous lessons.

Exit Slips: Exit Slip 9.1

Reasoning: The questions in the exit slips intend to review what they just learned about the closed and open circles. They can state the difference between them and their meaning. Then the rest of the questions are extended question which focuses on the student’s understanding of reverse statements of inequalities. The last question is intended to be a thinking task in which students will think of all the possible values that prove the inequality. My cooperating teacher told me that some students have still yet to cover the idea of infinity. So, I created the question to see if students would mention infinity and spark that idea within them. This is not for marks even though there are total marks indicated in the slips.

What Kind of Assessment (as, for, of)?

Formative Assessment: Assessment as Learning – Students assess themselves using the guided notes as well as my comments from their exit slips. My comments in the exit slips are for students to assess their understanding of the topic taught in today’s class as well as the previous classes.

Formative Assessment: Assessment for Learning – This exit slip will guide me with individual students’ understanding of inequality. This is a type of evidence that I take from my students to inform me about my teaching (if they understood) and their learning.

Bloom’s Taxonomy Category

Remembering – Students are recalling information from previous classes or the previous school year.

Understanding – Students summarize their knowledge through the exit slip.

Applying – Students apply their understanding in a complex setting.

Complexity

Easy: Guided Notes and first question of the exit slip

Medium: 2nd and 3rd questions of the exit slip because it requires more thinking and analysis.

Personal Growth

During those 8 weeks, I found that it is quite hard to come up with assessments when you have a bunch of students with different needs. Throughout my pre-internship, I tried my hardest to always have backup activities just in case something did not work out the way I intended to. I always thought that I always have to grade all the things that I do with my students. This made me realize that I am not giving them a chance to improve their learning or to fully understand the concept first before I evaluate it.

One of my goals is to enhance my skill in giving descriptive feedback. I think I achieved this when I was making comments on a student’s exit slips. I gave them feedback and suggestions on how to improve their thinking and answer the questions. and if their answer is right, I added some notes to consider going forward. It felt nice giving feedback and I hope that the students have read it so could self-assess as well.

I am looking forward to my 3-week pre-internship because I will have more authority on how to teach certain things and put my instruction into it.  I will probably be able to achieve one of my goals which is to implement different types of assessment in the classroom. Although I have done a variety, most of them are just different types of “check your understanding” activities. I would like to tackle more on assessments where students have created the criteria and can show their understanding in different ways.

 

ALL RIGHTS RESERVE TO THE OWNERS OF SOME OF THE TASKS I HAVE IMPLEMENTED IN MY CLASSROOM.